I think that the Monty Hall Problem is one of those litmus tests for how smart you really are. Not how many things you memorized or how much trivia you soaked up, but by how willing you are to change your assumptions when faced with data that contradicts those assumptions.
When I first encountered the Monty Hall Problem, I believed I knew the answer, but I was informed it was incorrect.
I then tested a few iterations on paper. My assumptions seemed wrong, but I wasn’t convinced.
I then wrote a short program that showed me what happened if I never changed my choice, and then what happened if I always changed my choice.
The data triumphed over my assumptions, but I was resistant because of my belief.
I’m marginally better now in that I tend to respond to such puzzles with an air of “Really? How does that work…?”
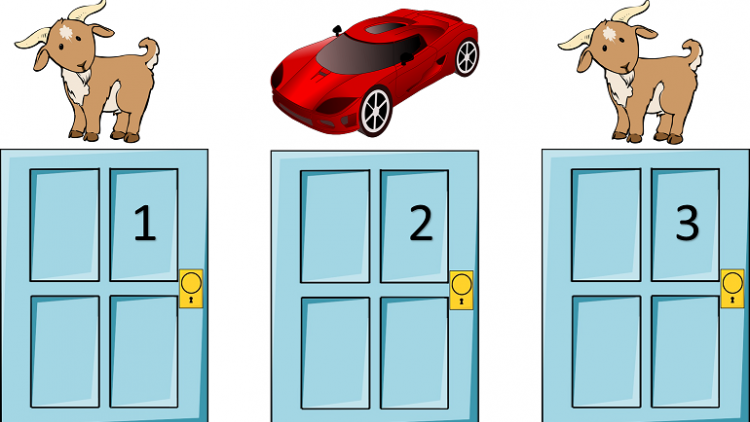
If you aren’t sure what the Monty Hall Problem is, or never heard of it, this is it in a nutshell:
A game show host shows you three doors. Behind one door is a fabulous new car. He asks you to pick a door and let him know which door you pick. He then looks behind the other doors and opens one you did not pick which has nothing behind it. You are now faced with two doors: the one you picked and one you did not pick. You know a fabulous new car is behind one of the doors. Do you change your guess?
The answer is that you should always change your guess. The odds that you’ve picked the correct door out of the set of doors is 1:3 and the odds of the car being behind any one of the doors in the remaining set are 2:3. These odds don’t change just because someone opens a door.
Most people believe that it doesn’t matter, that the odds magically shift to 1:2.
And that’s the difference, right there, between belief and data.
If you would like to learn more about the Monty Hall Problem, check out this basic introduction to The Monty Hall Problem on Wikipedia.